レイリー限界

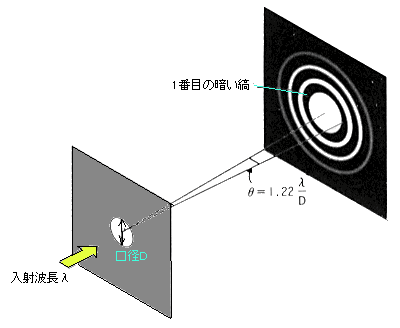
【　光の回折　】
●望遠鏡などの性能に分解能という言葉がある。「どのくらい細かなところまで見ることができるか」を表したもので、単位は角度の秒である。例えば口径100mmの望遠鏡では、1.16秒というように表す。この計算の元になっているのが、「ドーズ限界」というものだ。イギリスの火星観測者Ｗ．Ｒ，ドーズ（1799-1868）が用いた実験式　　θ”＝115.8”/Ｄ によるものだ。 これは、光の回折という現象によって引き起こされるもので、光が波であることから生じてくる。望遠鏡の前側の対物レンズを通った光は波の性質から、光の直進性からはずれた所まで広がってくる。普段、物の影を見たときに、はっきりした影の外側にうすぼんやりとやや暗くなった部分があるのに気がついたことがあるだろう。あれと同じことだ。 ●この回折現象によって、星みたいに理想的な点光源であっても、上の図のように大きさを持った明るい像の回りに暗いリングと明るいリングの模様ができてしまう。 中心像から1番目の暗いリングの中心までの距離が上図の角度θ（単位はラジアン）になる。これは、光の波長（色の違いと思えばいい）と望遠鏡対物レンズの口径で決まってしまう。角度の秒で表すと、 　　θ”＝251575”×λ/Ｄ になる。観測波長を肉眼に最も敏感な555ｎｍにすると、 　　θ”＝127.5”/Ｄ になる。 ●レイリ−限界（レイリーリミット）は、同じような明るさの２つの星が近くに見えているときに、それを２つの星であると認識できる限界を表したものだ。それはちょうど右図のように、第１の星の１番目の暗いリングのところに、２番目の星の明るい中心がきたときと定義した。星の明るさや望遠鏡の収差などによって、この計算通りにならないこともあるが、一種の取り決めと思えばいい。人によっては、この限界よりもさらに細かな角度まで見える人もいれば、逆の場合もありうる。レイリー限界は一種の目安である。 ●上図のθの式から想像できるように、口径が大きい程、θの値は小さくなるから、細かなところまで見えるようになる。また観測波長が短いものほど分解が上がることにもなる。赤い光よりも青い光、さらに肉眼では見えないＸ線が波長が短い。波長が長い電波では、分解能を上げるために、口径を大きくする必要が出てくる。	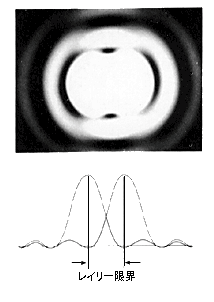【　２つの星のレイリー限界　】
＊レイリー　・・・　本名をＪ．Ｗ．ストラット（1842-1919）といい、イギリス生まれの物理学者であり、通称「ロード・レイリー」と呼ばれている。